What Is A Convolution Filter
How Do Convolutional Layers Work in Deep Learning Neural Networks?
Last Updated on April 17, 2020
Convolutional layers are the major building blocks used in convolutional neural networks.
A convolution is the simple application of a filter to an input that results in an activation. Repeated application of the same filter to an input results in a map of activations called a feature map, indicating the locations and strength of a detected feature in an input, such as an paradigm.
The innovation of convolutional neural networks is the ability to automatically learn a large number of filters in parallel specific to a preparation dataset under the constraints of a specific predictive modeling trouble, such equally image nomenclature. The result is highly specific features that tin exist detected anywhere on input images.
In this tutorial, you will discover how convolutions work in the convolutional neural network.
After completing this tutorial, you will know:
- Convolutional neural networks employ a filter to an input to create a feature map that summarizes the presence of detected features in the input.
- Filters tin be handcrafted, such every bit line detectors, but the innovation of convolutional neural networks is to larn the filters during training in the context of a specific prediction problem.
- How to summate the feature map for one- and two-dimensional convolutional layers in a convolutional neural network.
Kicking-start your project with my new volume Deep Learning for Estimator Vision, including step-past-footstep tutorials and the Python source code files for all examples.
Let's get started.

A Gentle Introduction to Convolutional Layers for Deep Learning Neural Networks
Photo by mendhak, some rights reserved.
Tutorial Overview
This tutorial is divided into four parts; they are:
- Convolution in Convolutional Neural Networks
- Convolution in Reckoner Vision
- Ability of Learned Filters
- Worked Example of Convolutional Layers
Want Results with Deep Learning for Reckoner Vision?
Accept my costless seven-day e-mail crash course now (with sample code).
Click to sign-up and likewise become a free PDF Ebook version of the course.
Convolution in Convolutional Neural Networks
The convolutional neural network, or CNN for brusque, is a specialized type of neural network model designed for working with two-dimensional image data, although they can be used with i-dimensional and three-dimensional data.
Primal to the convolutional neural network is the convolutional layer that gives the network its proper name. This layer performs an performance called a "convolution".
In the context of a convolutional neural network, a convolution is a linear performance that involves the multiplication of a gear up of weights with the input, much like a traditional neural network. Given that the technique was designed for two-dimensional input, the multiplication is performed betwixt an array of input data and a two-dimensional array of weights, called a filter or a kernel.
The filter is smaller than the input data and the blazon of multiplication applied betwixt a filter-sized patch of the input and the filter is a dot product. A dot product is the element-wise multiplication between the filter-sized patch of the input and filter, which is then summed, always resulting in a single value. Because information technology results in a single value, the operation is often referred to every bit the "scalar product".
Using a filter smaller than the input is intentional equally it allows the same filter (set of weights) to exist multiplied by the input array multiple times at different points on the input. Specifically, the filter is applied systematically to each overlapping part or filter-sized patch of the input data, left to right, meridian to bottom.
This systematic application of the same filter across an image is a powerful idea. If the filter is designed to observe a specific type of feature in the input, then the application of that filter systematically across the entire input epitome allows the filter an opportunity to discover that feature anywhere in the image. This capability is commonly referred to every bit translation invariance, eastward.g. the general involvement in whether the feature is present rather than where information technology was present.
Invariance to local translation can be a very useful property if we care more nearly whether some feature is present than exactly where information technology is. For example, when determining whether an paradigm contains a face, we demand not know the location of the eyes with pixel-perfect accuracy, we simply demand to know that at that place is an eye on the left side of the face and an middle on the right side of the confront.
— Page 342, Deep Learning, 2016.
The output from multiplying the filter with the input array one time is a unmarried value. As the filter is applied multiple times to the input array, the result is a two-dimensional array of output values that represent a filtering of the input. Equally such, the 2-dimensional output array from this operation is called a "feature map".
Once a characteristic map is created, we can pass each value in the characteristic map through a nonlinearity, such as a ReLU, much like nosotros do for the outputs of a fully continued layer.
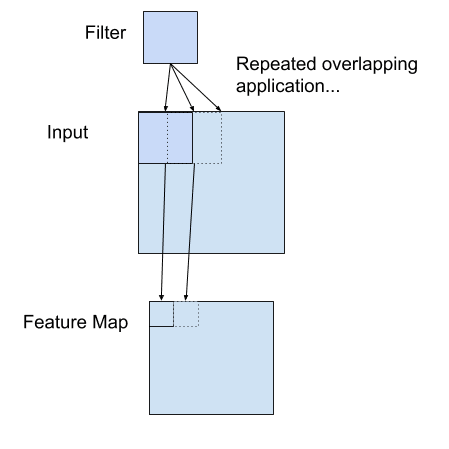
Example of a Filter Applied to a Two-Dimensional Input to Create a Feature Map
If y'all come from a digital betoken processing field or related area of mathematics, you may empathize the convolution functioning on a matrix equally something different. Specifically, the filter (kernel) is flipped prior to being applied to the input. Technically, the convolution as described in the use of convolutional neural networks is really a "cross-correlation". Nevertheless, in deep learning, it is referred to as a "convolution" operation.
Many machine learning libraries implement cantankerous-correlation but call information technology convolution.
— Page 333, Deep Learning, 2016.
In summary, we have a input, such as an image of pixel values, and we have a filter, which is a set of weights, and the filter is systematically applied to the input information to create a feature map.
Convolution in Computer Vision
The idea of applying the convolutional operation to paradigm data is not new or unique to convolutional neural networks; information technology is a common technique used in computer vision.
Historically, filters were designed by mitt by computer vision experts, which were then practical to an epitome to result in a characteristic map or output from applying the filter then makes the analysis of the image easier in some way.
For example, beneath is a hand crafted three×iii chemical element filter for detecting vertical lines:
| 0.0, 1.0, 0.0 0.0, one.0, 0.0 0.0, 1.0, 0.0 |
Applying this filter to an image volition outcome in a feature map that only contains vertical lines. It is a vertical line detector.
You tin can see this from the weight values in the filter; any pixels values in the center vertical line will be positively activated and whatsoever on either side will exist negatively activated. Dragging this filter systematically across pixel values in an image can only highlight vertical line pixels.
A horizontal line detector could as well be created and also practical to the image, for example:
| 0.0, 0.0, 0.0 one.0, i.0, one.0 0.0, 0.0, 0.0 |
Combining the results from both filters, e.g. combining both characteristic maps, volition result in all of the lines in an epitome existence highlighted.
A suite of tens or even hundreds of other minor filters tin exist designed to detect other features in the image.
The innovation of using the convolution performance in a neural network is that the values of the filter are weights to be learned during the grooming of the network.
The network will learn what types of features to excerpt from the input. Specifically, training under stochastic slope descent, the network is forced to learn to extract features from the image that minimize the loss for the specific task the network is being trained to solve, e.g. extract features that are the most useful for classifying images as dogs or cats.
In this context, you can see that this is a powerful thought.
Ability of Learned Filters
Learning a single filter specific to a car learning job is a powerful technique.
Nevertheless, convolutional neural networks achieve much more in practice.
Multiple Filters
Convolutional neural networks do not learn a single filter; they, in fact, learn multiple features in parallel for a given input.
For instance, information technology is common for a convolutional layer to learn from 32 to 512 filters in parallel for a given input.
This gives the model 32, or fifty-fifty 512, different means of extracting features from an input, or many unlike ways of both "learning to come across" and after training, many unlike means of "seeing" the input data.
This multifariousness allows specialization, e.g. not just lines, just the specific lines seen in your specific grooming data.
Multiple Channels
Colour images have multiple channels, typically one for each color channel, such every bit cerise, green, and bluish.
From a data perspective, that ways that a unmarried prototype provided as input to the model is, in fact, 3 images.
A filter must always have the aforementioned number of channels as the input, often referred to every bit "depth". If an input image has 3 channels (e.g. a depth of iii), and so a filter applied to that paradigm must also accept 3 channels (e.1000. a depth of 3). In this case, a 3×three filter would in fact be 3x3x3 or [3, three, 3] for rows, columns, and depth. Regardless of the depth of the input and depth of the filter, the filter is applied to the input using a dot product operation which results in a single value.
This means that if a convolutional layer has 32 filters, these 32 filters are not just ii-dimensional for the two-dimensional image input, but are likewise three-dimensional, having specific filter weights for each of the 3 channels. Yet, each filter results in a single feature map. Which ways that the depth of the output of applying the convolutional layer with 32 filters is 32 for the 32 feature maps created.
Multiple Layers
Convolutional layers are not just applied to input data, e.thousand. raw pixel values, but they can as well exist applied to the output of other layers.
The stacking of convolutional layers allows a hierarchical decomposition of the input.
Consider that the filters that operate directly on the raw pixel values will acquire to extract low-level features, such as lines.
The filters that operate on the output of the first line layers may excerpt features that are combinations of lower-level features, such every bit features that comprise multiple lines to express shapes.
This process continues until very deep layers are extracting faces, animals, houses, and and so on.
This is exactly what nosotros meet in practise. The abstraction of features to high and higher orders as the depth of the network is increased.
Worked Example of Convolutional Layers
The Keras deep learning library provides a suite of convolutional layers.
We tin can better understand the convolution performance by looking at some worked examples with contrived information and handcrafted filters.
In this department, we'll wait at both a ane-dimensional convolutional layer and a two-dimensional convolutional layer example to both make the convolution operation physical and provide a worked instance of using the Keras layers.
Example of 1D Convolutional Layer
We tin can define a one-dimensional input that has eight elements all with the value of 0.0, with a two element crash-land in the centre with the values 1.0.
The input to Keras must be three dimensional for a 1D convolutional layer.
The beginning dimension refers to each input sample; in this case, we only have ane sample. The 2nd dimension refers to the length of each sample; in this instance, the length is eight. The tertiary dimension refers to the number of channels in each sample; in this case, we just accept a single channel.
Therefore, the shape of the input array will exist [1, eight, 1].
| # ascertain input data data = asarray ( [ 0 , 0 , 0 , ane , ane , 0 , 0 , 0 ] ) data = data . reshape ( 1 , 8 , 1 ) |
We volition ascertain a model that expects input samples to accept the shape [eight, ane].
The model will have a single filter with the shape of three, or 3 elements wide. Keras refers to the shape of the filter as the kernel_size.
| # create model model = Sequential ( ) model . add ( Conv1D ( i , three , input_shape = ( eight , one ) ) ) |
Past default, the filters in a convolutional layer are initialized with random weights. In this contrived example, we will manually specify the weights for the single filter. We will define a filter that is capable of detecting bumps, that is a high input value surrounded by depression input values, equally nosotros defined in our input case.
The three element filter we will define looks as follows:
The convolutional layer likewise has a bias input value that besides requires a weight that we volition set to zero.
Therefore, we tin can strength the weights of our ane-dimensional convolutional layer to use our handcrafted filter equally follows:
| # define a vertical line detector weights = [ asarray ( [ [ [ 0 ] ] , [ [ ane ] ] , [ [ 0 ] ] ] ) , asarray ( [ 0.0 ] ) ] # shop the weights in the model model . set_weights ( weights ) |
The weights must be specified in a iii-dimensional structure, in terms of rows, columns, and channels. The filter has a single row, three columns, and i channel.
Nosotros can recollect the weights and confirm that they were set correctly.
| # confirm they were stored print ( model . get_weights ( ) ) |
Finally, we tin apply the unmarried filter to our input data.
We tin can achieve this by calling the predict() function on the model. This volition return the feature map directly: that is the output of applying the filter systematically across the input sequence.
| # employ filter to input data yhat = model . predict ( information ) print ( yhat ) |
Tying all of this together, the complete example is listed below.
| 1 2 3 iv five vi 7 8 ix 10 11 12 xiii 14 15 sixteen 17 18 nineteen | # example of calculation 1d convolutions from numpy import asarray from keras . models import Sequential from keras . layers import Conv1D # define input information data = asarray ( [ 0 , 0 , 0 , one , one , 0 , 0 , 0 ] ) data = data . reshape ( ane , 8 , i ) # create model model = Sequential ( ) model . add ( Conv1D ( i , three , input_shape = ( 8 , 1 ) ) ) # define a vertical line detector weights = [ asarray ( [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] ) , asarray ( [ 0.0 ] ) ] # store the weights in the model model . set_weights ( weights ) # confirm they were stored print ( model . get_weights ( ) ) # apply filter to input data yhat = model . predict ( data ) print ( yhat ) |
Running the example first prints the weights of the network; that is the confirmation that our handcrafted filter was set in the model as we expected.
Next, the filter is applied to the input blueprint and the feature map is calculated and displayed. We can see from the values of the characteristic map that the bump was detected correctly.
| [array([[[0.]], [[one.]], [[0.]]], dtype=float32), assortment([0.], dtype=float32)] [[[0.] [0.] [one.] [ane.] [0.] [0.]]] |
Let's take a closer look at what happened here.
Remember that the input is an eight element vector with the values: [0, 0, 0, 1, 1, 0, 0, 0].
First, the 3-element filter [0, 1, 0] was applied to the outset three inputs of the input [0, 0, 0] by calculating the dot product ("." operator), which resulted in a single output value in the feature map of zero.
Think that a dot product is the sum of the element-wise multiplications, or here it is (0 x 0) + (1 x 0) + (0 x 0) = 0. In NumPy, this can be implemented manually as:
| from numpy import asarray impress ( asarray ( [ 0 , 1 , 0 ] ) . dot ( asarray ( [ 0 , 0 , 0 ] ) ) ) |
In our transmission example, this is every bit follows:
| [0, 1, 0] . [0, 0, 0] = 0 |
The filter was then moved along 1 element of the input sequence and the process was repeated; specifically, the same filter was applied to the input sequence at indexes 1, 2, and 3, which besides resulted in a zero output in the feature map.
| [0, 1, 0] . [0, 0, 1] = 0 |
We are beingness systematic, then over again, the filter is moved forth i more element of the input and applied to the input at indexes ii, 3, and 4. This time the output is a value of i in the characteristic map. Nosotros detected the feature and activated appropriately.
| [0, ane, 0] . [0, 1, 1] = ane |
The process is repeated until we calculate the entire feature map.
Annotation that the characteristic map has six elements, whereas our input has viii elements. This is an artefact of how the filter was practical to the input sequence. In that location are other ways to apply the filter to the input sequence that changes the shape of the resulting feature map, such as padding, but nosotros will not discuss these methods in this mail service.
You can imagine that with unlike inputs, we may notice the feature with more than or less intensity, and with different weights in the filter, that we would detect different features in the input sequence.
Case of 2d Convolutional Layer
We can expand the bump detection example in the previous section to a vertical line detector in a two-dimensional image.
Again, nosotros can constrain the input, in this case to a square eight×8 pixel input image with a unmarried channel (e.g. grayscale) with a single vertical line in the middle.
| [0, 0, 0, 1, one, 0, 0, 0] [0, 0, 0, i, 1, 0, 0, 0] [0, 0, 0, one, 1, 0, 0, 0] [0, 0, 0, 1, one, 0, 0, 0] [0, 0, 0, one, 1, 0, 0, 0] [0, 0, 0, 1, 1, 0, 0, 0] [0, 0, 0, 1, 1, 0, 0, 0] [0, 0, 0, i, 1, 0, 0, 0] |
The input to a Conv2D layer must exist four-dimensional.
The showtime dimension defines the samples; in this case, there is simply a single sample. The 2d dimension defines the number of rows; in this case, eight. The third dimension defines the number of columns, again viii in this case, and finally the number of channels, which is one in this case.
Therefore, the input must accept the 4-dimensional shape [samples, rows, columns, channels] or [ane, 8, eight, i] in this case.
| # ascertain input information data = [ [ 0 , 0 , 0 , 1 , i , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , i , 0 , 0 , 0 ] , [ 0 , 0 , 0 , i , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , i , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , i , 1 , 0 , 0 , 0 ] ] data = asarray ( data ) data = data . reshape ( 1 , eight , 8 , 1 ) |
We will ascertain the Conv2D with a unmarried filter as we did in the previous section with the Conv1D example.
The filter will be two-dimensional and square with the shape three×3. The layer will await input samples to have the shape [columns, rows, channels] or [8,eight,1].
| # create model model = Sequential ( ) model . add together ( Conv2D ( ane , ( 3 , 3 ) , input_shape = ( viii , viii , 1 ) ) ) |
We will ascertain a vertical line detector filter to detect the single vertical line in our input data.
The filter looks as follows:
Nosotros tin can implement this as follows:
| # define a vertical line detector detector = [ [ [ [ 0 ] ] , [ [ ane ] ] , [ [ 0 ] ] ] , [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] , [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] ] weights = [ asarray ( detector ) , asarray ( [ 0.0 ] ) ] # store the weights in the model model . set_weights ( weights ) # confirm they were stored impress ( model . get_weights ( ) ) |
Finally, we will use the filter to the input image, which will result in a feature map that nosotros would look to show the detection of the vertical line in the input image.
| # apply filter to input data yhat = model . predict ( data ) |
The shape of the feature map output volition be four-dimensional with the shape [batch, rows, columns, filters]. We will exist performing a single batch and we accept a single filter (one filter and ane input channel), therefore the output shape is [1, ?, ?, one]. We tin can pretty-print the content of the single characteristic map as follows:
| for r in range ( yhat . shape [ 1 ] ) : # print each column in the row print ( [ yhat [ 0 , r , c , 0 ] for c in range ( yhat . shape [ ii ] ) ] ) |
Tying all of this together, the complete example is listed below.
| one ii 3 iv 5 6 7 eight nine 10 11 12 13 14 15 16 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 xxx 31 32 | # example of calculation 2d convolutions from numpy import asarray from keras . models import Sequential from keras . layers import Conv2D # ascertain input data information = [ [ 0 , 0 , 0 , 1 , one , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , i , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , one , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] , [ 0 , 0 , 0 , 1 , 1 , 0 , 0 , 0 ] ] data = asarray ( data ) data = data . reshape ( 1 , viii , 8 , 1 ) # create model model = Sequential ( ) model . add ( Conv2D ( 1 , ( 3 , 3 ) , input_shape = ( 8 , eight , 1 ) ) ) # define a vertical line detector detector = [ [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] , [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] , [ [ [ 0 ] ] , [ [ 1 ] ] , [ [ 0 ] ] ] ] weights = [ asarray ( detector ) , asarray ( [ 0.0 ] ) ] # store the weights in the model model . set_weights ( weights ) # confirm they were stored print ( model . get_weights ( ) ) # utilise filter to input data yhat = model . predict ( data ) for r in range ( yhat . shape [ 1 ] ) : # print each column in the row print ( [ yhat [ 0 , r , c , 0 ] for c in range ( yhat . shape [ 2 ] ) ] ) |
Running the example first confirms that the handcrafted filter was correctly defined in the layer weights
Adjacent, the calculated feature map is printed. We can meet from the calibration of the numbers that indeed the filter has detected the single vertical line with stiff activation in the middle of the characteristic map.
| [array([[[[0.]], [[one.]], [[0.]]], [[[0.]], [[1.]], [[0.]]], [[[0.]], [[1.]], [[0.]]]], dtype=float32), array([0.], dtype=float32)] [0.0, 0.0, three.0, 3.0, 0.0, 0.0] [0.0, 0.0, 3.0, 3.0, 0.0, 0.0] [0.0, 0.0, 3.0, 3.0, 0.0, 0.0] [0.0, 0.0, 3.0, iii.0, 0.0, 0.0] [0.0, 0.0, 3.0, 3.0, 0.0, 0.0] [0.0, 0.0, 3.0, 3.0, 0.0, 0.0] |
Let'south take a closer look at what was calculated.
First, the filter was applied to the top left corner of the prototype, or an prototype patch of 3×3 elements. Technically, the paradigm patch is three dimensional with a single channel, and the filter has the same dimensions. We cannot implement this in NumPy using the dot() function, instead, we must use the tensordot() function and so we can appropriately sum across all dimensions, for example:
| from numpy import asarray from numpy import tensordot m1 = asarray ( [ [ 0 , i , 0 ] , [ 0 , 1 , 0 ] , [ 0 , i , 0 ] ] ) m2 = asarray ( [ [ 0 , 0 , 0 ] , [ 0 , 0 , 0 ] , [ 0 , 0 , 0 ] ] ) print ( tensordot ( m1 , m2 ) ) |
This adding results in a unmarried output value of 0.0, east.g., the characteristic was not detected. This gives us the offset element in the top-left corner of the characteristic map.
Manually, this would exist equally follows:
| 0, i, 0 0, 0, 0 0, 1, 0 . 0, 0, 0 = 0 0, 1, 0 0, 0, 0 |
The filter is moved along one cavalcade to the left and the process is repeated. Once more, the feature is not detected.
| 0, 1, 0 0, 0, 1 0, ane, 0 . 0, 0, one = 0 0, ane, 0 0, 0, 1 |
One more move to the left to the next column and the feature is detected for the first time, resulting in a strong activation.
| 0, i, 0 0, 1, 1 0, 1, 0 . 0, 1, 1 = three 0, 1, 0 0, one, one |
This process is repeated until the edge of the filter rests against the border or terminal column of the input image. This gives the concluding element in the offset full row of the feature map.
| [0.0, 0.0, 3.0, 3.0, 0.0, 0.0] |
The filter then moves downwards ane row and back to the first column and the process is related from left to right to give the second row of the characteristic map. And on until the bottom of the filter rests on the bottom or last row of the input image.
Once again, as with the previous section, we can meet that the feature map is a six×6 matrix, smaller than the 8×8 input prototype because of the limitations of how the filter tin exist practical to the input image.
Further Reading
This section provides more resource on the topic if you lot are looking to go deeper.
Posts
- Crash Course in Convolutional Neural Networks for Machine Learning
Books
- Chapter 9: Convolutional Networks, Deep Learning, 2016.
- Chapter five: Deep Learning for Computer Vision, Deep Learning with Python, 2017.
API
- Keras Convolutional Layers API
- numpy.asarray API
Summary
In this tutorial, you lot discovered how convolutions work in the convolutional neural network.
Specifically, yous learned:
- Convolutional neural networks apply a filter to an input to create a feature map that summarizes the presence of detected features in the input.
- Filters tin can be handcrafted, such as line detectors, but the innovation of convolutional neural networks is to larn the filters during training in the context of a specific prediction problem.
- How to calculate the characteristic map for one- and two-dimensional convolutional layers in a convolutional neural network.
Practise yous accept any questions?
Ask your questions in the comments beneath and I will do my best to answer.
What Is A Convolution Filter,
Source: https://machinelearningmastery.com/convolutional-layers-for-deep-learning-neural-networks/
Posted by: moorekrounist.blogspot.com



0 Response to "What Is A Convolution Filter"
Post a Comment